システムの常微分方程式

当研究所のブログ「前進オイラー解法」「アダプティブ時間積分」では未知関数が１個の常微分方程式（ODE)を扱いました。
ここではシステムを記述する際に出てくる複数の未知関数を含む連立常微分方程式について見ていきます。数値解法はアダプティブ時間積分法を使いました。

いま、２枚の固定壁の間に質点\( m_{1} \)と\( m_{2} \)があり、壁と\( m_{1} \)の間はバネ定数\( k_{1} \)のバネで、質点\( m_{1} \)と\( m_{2} \)の間はバネ定数\( k_{2} \)のバネで、質点\( m_{2} \) ともう一枚の壁との間はバネ定数\( k_{3} \)のバネでつながっているとします。
各質点の位置を\( x{1} \)と\( x_{2} \) とした時、それらの時間変化を決める方程式は次の式に
なります。

\[ m_{1} \ddot{x_{1}} = – k_{1} x_{1} – k_{2} ( x_{1} – x_{2} ) \]

\[ m_{2} \ddot{x_{2}} = – k_{2} (x_{2} – x_{1})- k_{3} x_{2} \]

この連立方程式をPythonで解いてみます。

Python

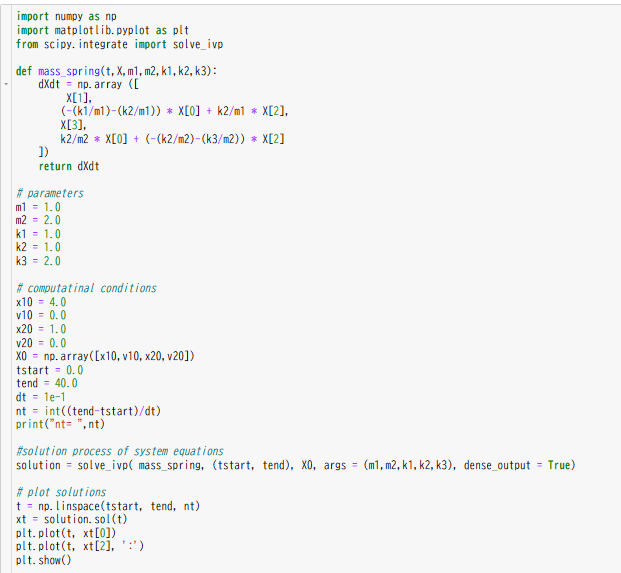
結果

初期値を変更して３ケースを計算しました。いずれのケースも次のパラメータとしました。

\[ (m_{1}, m_{2} ) = (1,2), (k_{1}, k_{2}, k_{3} )= (1, 1, 2) \]

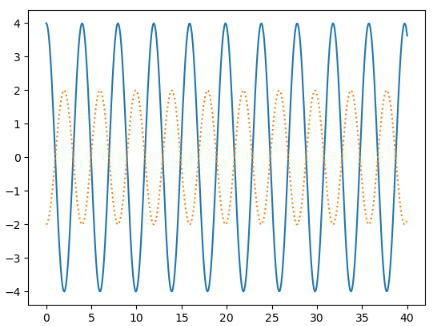
プロットの横軸は時間であり、縦軸は各質点の変位であり、実線が\(x_{1} \)、点線が\( x_{2} \) です。

ケース１　

\[ (x_{10}, v_{10},x_{20}, v_{20} ) = (4, 0, 1, 0) \]

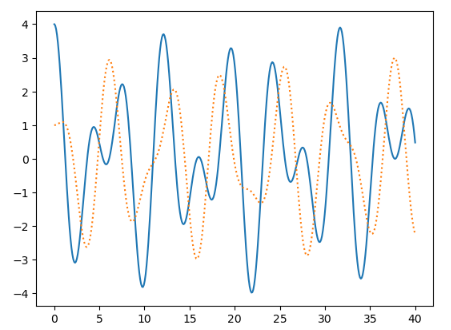
ケース２

\[ (x_{10}, v_{10},x_{20}, v_{20} ) = (4, 0, 4, 0) \]

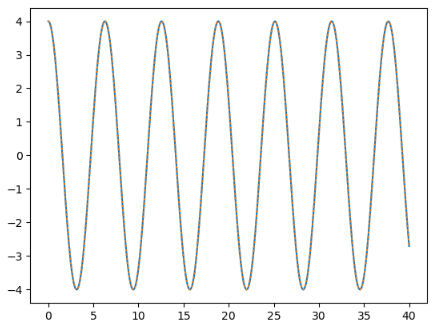
ケース３

\[(x_{10}, v_{10},x_{20}, v_{20} ) = (4, 0, -2, 0) \]