アダプティブ時間積分

当研究所のブログ「前進オイラー解法」で紹介した数値解法では、
時間積分幅\( dt \)が一定であり、精度よく計算をしようとすると、
解の性質に関わらず、細かな時間積分幅を時間全域において使う必要があります。
これでは計算時間がかかってしまいます。
一方で、解の変化が大きい個所では時間積分幅を小さく、そうでないところは時間積分幅を
大きくとるということが自動的にできれば、計算時間を短縮できそうです。
そのような手法に適応時間刻み幅制御があります。アダプティブ時間積分法とも呼ばれます。

Python

scipy.integrate import solve_ivp でアダプティブ時間積分法を読み込みます。

利用法

solution = solve_ivp( ODE右辺, (開始時刻, 終了時刻)，初期値配列，dense_output = True)

結果

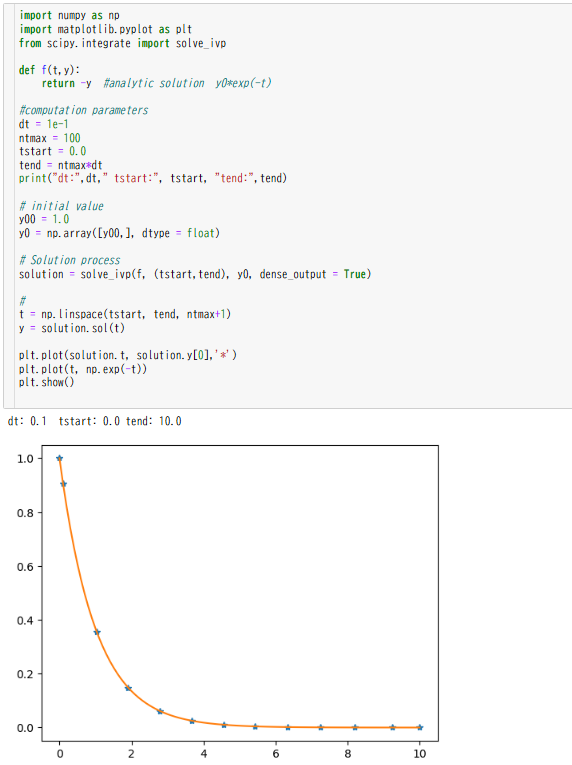
前進オイラー解法に比べてわずか13点の計算点の利用という結果になりました。
ここでは、解析解があるので、solve_ivpの結果はそのままシンボルでプロットし、解析解を描画することで両者が一致しているかどうかを確かめています。

利用上の注意

解析解がない場合、solve_ivpの出力 solution.tとsolution.y[0]を使ってプロットすると、不等間隔の時間積分幅でプロットされ、解の形がわかりにくいので、描画したい時刻\( t \)を自作し、その時刻に対応する数値解を補間計算solution.sol(t)によって採取し、描画するとよい。